Optipedia • SPIE Press books opened for your reference.
Wavefront Expansion
Excerpt from Field Guide to Geometrical Optics
The wavefront expansion is a power series expansion for thewavefront aberrations inherent to a rotationally symmetricoptical system. These aberrations are inherent to the design ofthe system. In order to satisfy the requirements of rotationalsymmetry, the expansion terms are H2, ρ2 and Hρ cosθ. The coefficient subscript encodes the powers of the corresponding polynomial term:
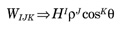
| W = W020ρ2 | Defocus |
| + W111Hρ cosθ | Wavefront tilt |
Third-Order Terms
| + W040ρ4 | Spherical aberration (SA) |
| + W131Hρ3 cosθ | Coma |
| + W222H2ρ2 cos2 θ | Astigmatism |
| + W220H2ρ2 | Field curvature |
| + W311H3ρ cosθ | Distortion |
Fifth-Order Terms
| + W060ρ6 | Fifth-order SA |
| + W151Hρ5cosθ | Fifth-order linear coma |
| + W422H4ρ2cos2θ | Fifth-order astigmatism |
| + W420H4ρ2 | Fifth-order field curvature |
| + W511H5ρcosθ | Fifth-order distortion |
| + W240H2ρ4 | Sagittal oblique SA |
| + W242H2ρ4cos2θ | Tangential oblique SA |
| + W331H3ρ3cosθ | Cubic coma |
| } Elliptical coma | |
| + W333H3ρ3cos3θ | Line coma |
| + Higher order terms |
The wavefront terms are denoted by the order of their rayaberration, which is one less than the wavefront aberrationorder. Terms with no pupil dependence, piston (W000) and field-dependent phase (W200,W400, etc.), are usually ignored.
Citation:
View SPIE terms of use.
J. E. Greivenkamp, Field Guide to Geometrical Optics, SPIE Press, Bellingham, WA (2004).
View SPIE terms of use.
Excerpt from

